

We refer to $£A$ as the principal balance. Simple and Compound Interest Simple Interest For example, \ so the sequence is neither arithmetic nor geometric.
Formulas for arithmetic sequences series#
A series does not have to be the sum of all the terms in a sequence. The starting index is written underneath and the final index above, and the sequence to be summed is written on the right. We call the sum of the terms in a sequence a series. The Summation Operator, $\sum$, is used to denote the sum of a sequence. If the dots have nothing after them, the sequence is infinite. If the dots are followed by a final number, the sequence is finite. Note: The 'three dots' notation stands in for missing terms. is a finite sequence whose end value is $19$.Īn infinite sequence is a sequence in which the terms go on forever, for example $2, 5, 8, \dotso$. For example, $1, 3, 5, 7, 9$ is a sequence of odd numbers.Ī finite sequence is a sequence which ends. Therefore sum of first 12 odd natural numbers will be 144.Contents Toggle Main Menu 1 Sequences 2 The Summation Operator 3 Rules of the Summation Operator 3.1 Constant Rule 3.2 Constant Multiple Rule 3.3 The Sum of Sequences Rule 3.4 Worked Examples 4 Arithmetic sequence 4.1 Worked Examples 5 Geometric Sequence 6 A Special Case of the Geometric Progression 6.1 Worked Examples 7 Arithmetic or Geometric? 7.1 Arithmetic? 7.2 Geometric? 8 Simple and Compound Interest 8.1 Simple Interest 8.2 Compound Interest 8.3 Worked Examples 9 Video Examples 10 Test Yourself 11 External Resources SequencesĪ sequence is a list of numbers which are written in a particular order. Now, formula for sum of n terms in arithmetic sequence is: Solution: As we know that the required sequence will be: Q.2: Find the sum of the first 12 odd natural numbers. Therefore 15th term in the sequence will be 28. Q.1: Find the 15th term in the arithmetic sequence given as 0, 2, 4, 6, 8, 10, 12, 14….?
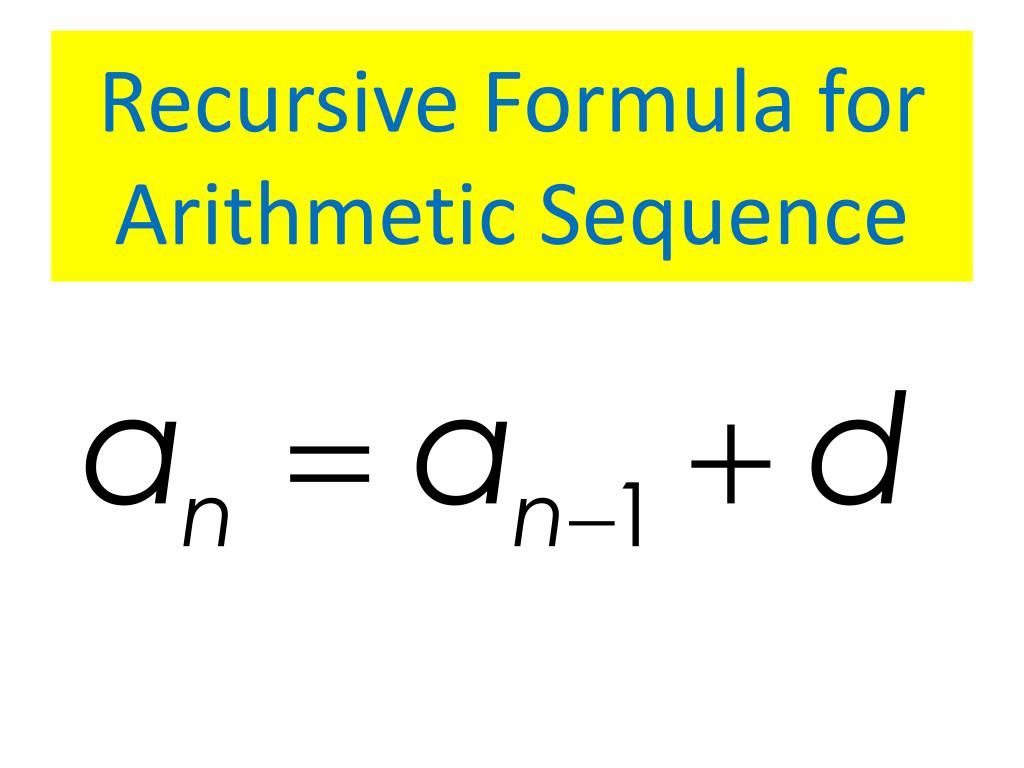

Solved Examples for Arithmetic Sequence Formula Sum of n terms of the arithmetic sequence can be computed as:

\(a_n = a + (n – 1)d\) 2] Sum of n terms in the arithmetic sequence In general, the nth term of the arithmetic sequence, given the first term ‘a’ and common difference ‘d ’ will be as follows: Arithmetic Sequence Formula 1] The formula for the nth general term of the sequence If the sequence is 2, 4, 6, 8, 10, …, then the sum of first 3 terms: Also, the sum of the terms of a sequence is called a series, can be computed by using formulae. Thus we can see that series and finding the sum of the terms of series is a very important task in mathematics.Īrithmetic sequence formulae are used to calculate the nth term of it. Such formulae are derived by applying simple properties of the sequence. We can compute the sum of the terms in such an arithmetic sequence by using a simple formula. An arithmetic progression is a type of sequence, in which each term is a certain number larger than the previous term. Therefore, the difference between the adjacent terms in the arithmetic sequence will be the same. An arithmetic sequence is a sequence in which each term is created or obtained by adding or subtracting a common number to its preceding term. 3 Solved Examples for Arithmetic Sequence Formula Definition of Arithmetic Sequenceįormally, a sequence can be defined as a function whose domain is set of the first n natural numbers, constant difference between terms.


 0 kommentar(er)
0 kommentar(er)
